一. 前言:
1.1 二叉搜索树的缺陷:
如果插入一连串连续的数据,如下图所示:

形成了一颗非平衡树:
- 比较好的二叉搜索树应该是左右分布均匀的;
- 但是插入连续数据后,分布的不均匀,变成非平衡树;
- 对于一颗平衡二叉树来说,插入或查找等的操作效率是O(logN);
- 对于一颗非平衡二叉树,相当于编写了一个链表,查找效率变成了O(N);
1.2 常见的平衡树
为了能以较快的时间O(logN)来操作一棵树,我们需要保证树尽量是平衡的,时间复杂度接近O(logN);
常见的平衡树有哪些呢?
AVL树
- AVL树是最早的一种平衡树,它有办法保持树的平衡(每个节点多存储了一个额外的数据);
- 因为AVL树是平衡的,所以时间复杂度也是O(logN);
- 但是,每次插入或删除操作相对于红黑树来说都不高,整体效率不如红黑树;
红黑树
- 红黑树也通过一些特性来保持树的平衡;
- 因为是平衡树,所以时间复杂度也是O(logN);
- 每次插入或删除操作,红黑树性能优于AVL树,所以现在平衡树的应用基本都是红黑树。
二. 认识红黑树
2.1 邂逅红黑树
首先,红黑树很难,难到什么程度呢?
- 数据结构中一个难点中的难点;
- 数据结构很难,红黑树将难度上升了一个档次;
ok,在这里,一起来踏入数据结构红黑树这块禁区。
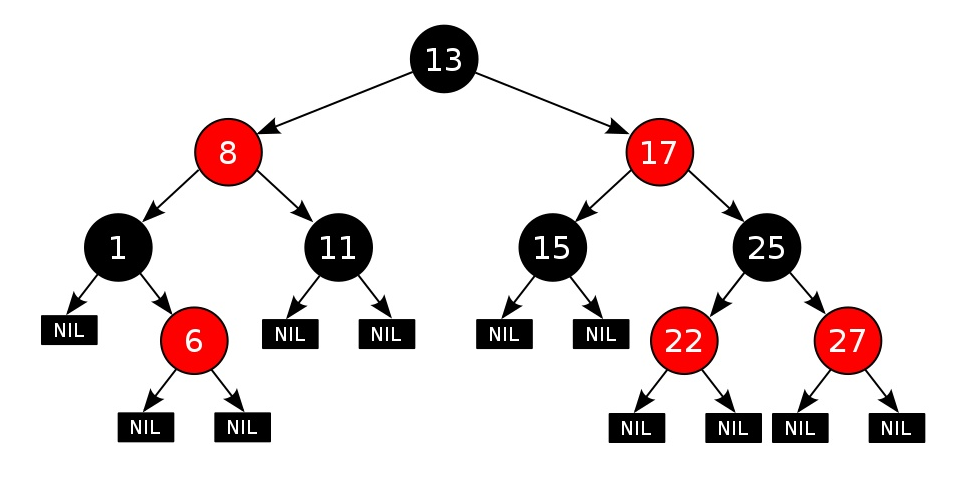
2.2 红黑树的规则
红黑树除了符合二叉搜索树的基本规则外,还添加了以下特性:
- 节点是黑色或红色;
- 根节点是黑色;
- 每个叶子节点都是黑色的空节点(NIL节点);
- 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
- 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
2.3 红黑树的相对平衡
前面的约束,确保了红黑树的关键特性:
- 从根叶子的最长路径,不会超过最短可能路径的两倍长;
- 结果就是这个树基本是平衡的;
- 虽然没有做到绝对的平衡,但是可以保证在最坏的情况下,依然是高效的;
为什么可以做到最长路径不会超过最短路径的两倍呢?
- 特性4决定了路径不能有两个相连的红色节点;
- 最短的可能路径都是黑色节点;
- 最长的可能路径是红色和黑色交替;
- 特性5所有路径都有相同数目的黑色节点;
- 这就表明了没有路径能多余任何其他路径的两倍长;
三. 红黑树的变换
插入一个新节点时,有可能树不再平衡,可以通过三种方式的变换让树保持平衡:
3.1 变色:
为了重新符合红黑树的规则,尝试把红色节点变为黑色,或者把黑色节点变为红色;
- 首先需要知道插入的新的节点通常都是红色节点
- 因为在插入节点为红色的时候,有可能不违反红黑树任何规则;
- 而插入黑色节点,必然会导致一条路径上多了黑色节点,这是很难调整的;
- 红色节点可能导致出现红红相连的情况,但是这种情况可以通过颜色调换和旋转来调整。
3.2 旋转
3.2.1 左旋转
逆时针旋转红黑树的两个节点,使得父节点被自己的右孩子取代,而自己成为自己的左孩子。
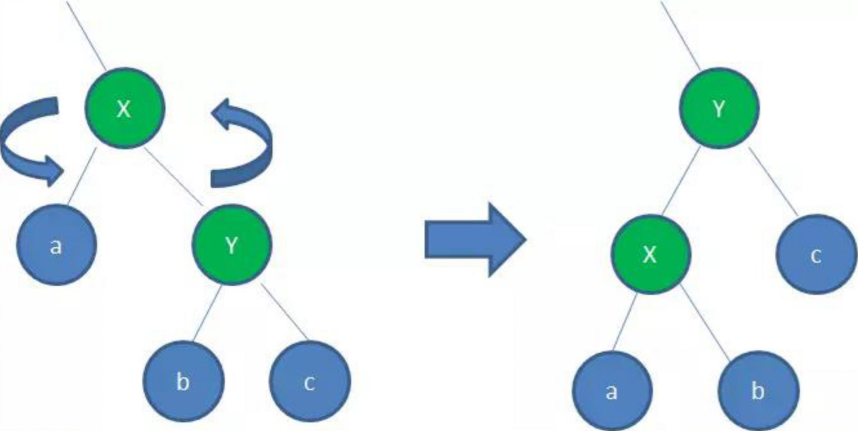
图中,身为右孩子的Y取代了X的位置,而X变成了Y的左孩子,把b推过来,此为左旋转。
3.2.2 右旋转
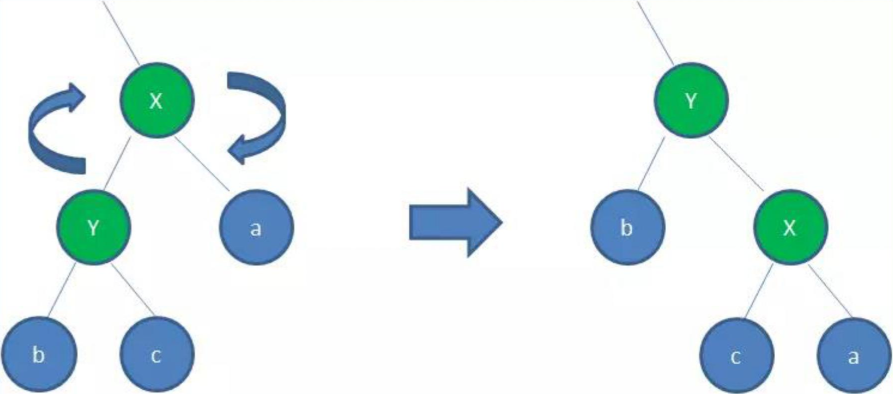
图中,身为左孩子的Y取代了X的位置,而X变成了Y的右孩子,把c推过来,此为右旋转。
如果它们有子树也不影响旋转。
四. 插入操作的情况分析
设要插入的节点为N,其父节点为P,祖父节点为G,其兄弟节点为U(即P和U是同一个节点的子节点)
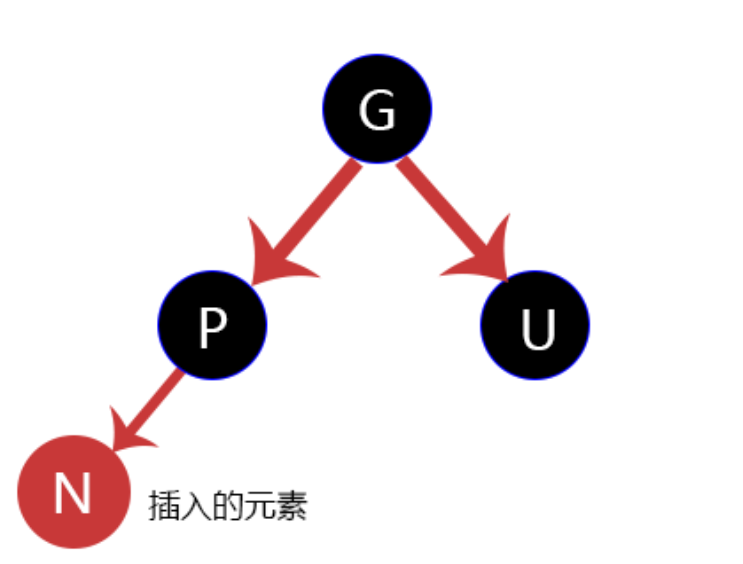
4.1 情况一
新节点N位于树的根上,没有父节点。
- 这种情况下,我们直接将红色变换成黑色即可,这样满足特性2
4.2 情况二
新节点的父节点P是黑色。
- 特性4没有失效(新节点是红色的),特性5也没有问题;
- 尽管新节点N有两个黑色的叶子节点nil,但是新节点N是红色的,所以通过它的路径中黑色节点的个数依然相同,满足特性5。
4.3 情况三
- P为红色,U也是红色;
- 父红叔红祖黑 转换为 父黑叔黑祖红
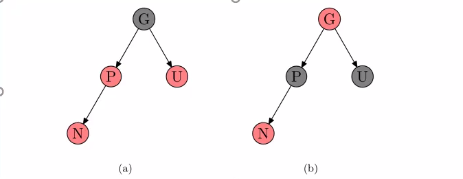
可能出现的问题:
- N的祖父节点,G的父节点也可能是红色,这就违反了特性3,可以递归调整颜色;
- 如果递归调整到了根节点,就需要进行旋转了,文章最后例子中会遇到这个问题。
4.4 情况四
- N的叔叔U是黑节点,且N是左孩子;
- 父红叔黑祖黑,N是左孩子。
需要转为:父黑 祖红 再右旋转
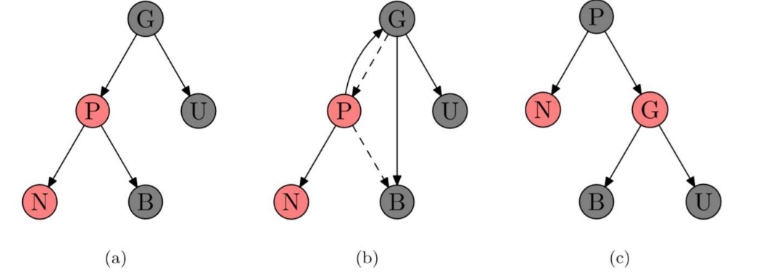
操作流程
- 交换以前的父节点P和祖父节点G的颜色(P为黑色,G变成红色。G原来一定是黑色);
- 对祖父节点进行依次右旋转;
- 旋转后的树中,以前父节点P现在是N之前祖父节点G的父节点;
- B节点向右平移,成为G节点的左子节点。
4.5 情况五
- N的叔叔U是黑节点,且N是右孩子;
- 父红叔黑祖黑,N是右孩子。
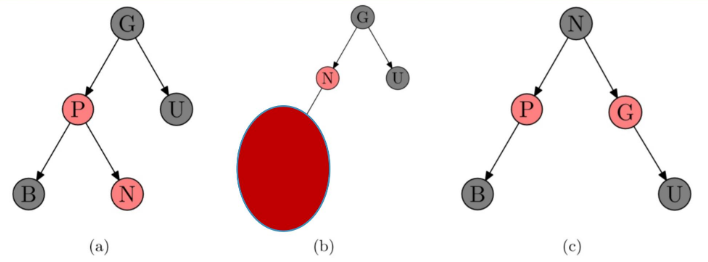
操作方案:
- 对P节点进行依次左旋转,形成情况四的结果;
- 对祖父节点G进行依次右旋转,并且改变颜色即可
操作流程:
以P为根,左旋转;
- 将P作为新插入的红色节点考虑即可
- 自己变成黑色;
- 祖变成红色;
- 以祖为根,进行右旋转。
五. 红黑树的案例
案例:依次插入10 9 8 7 6 5 4 3 2 1 。
模拟对树的操作:https://www.cs.usfca.edu/~galles/visualization/RedBlack.html
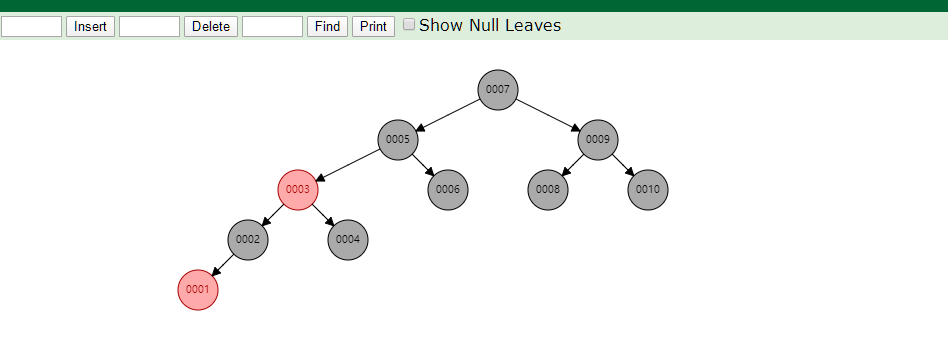
开始
插入10
- 将节点10的颜色改成黑色。
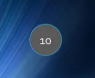
插入9
- 符合情况2
- 不需要任何变化
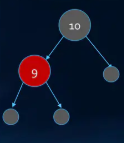
插入8
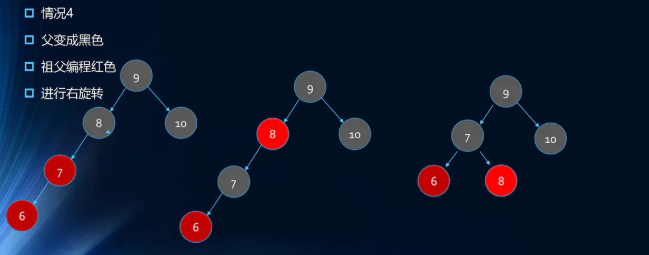
- 符合情况4
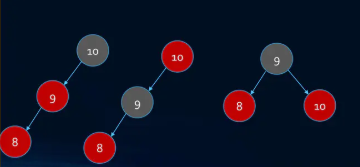
插入7
- 符合情况3;
- 变颜色后根节点为红,需要变黑。
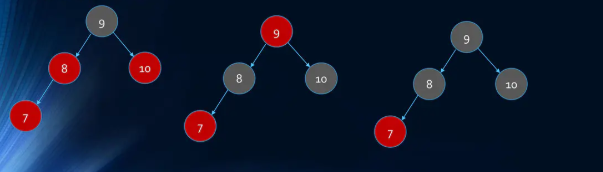
- 插入6
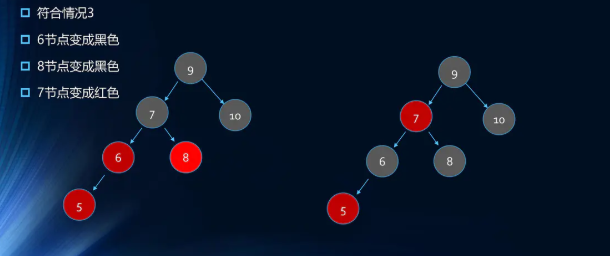
- 插入5
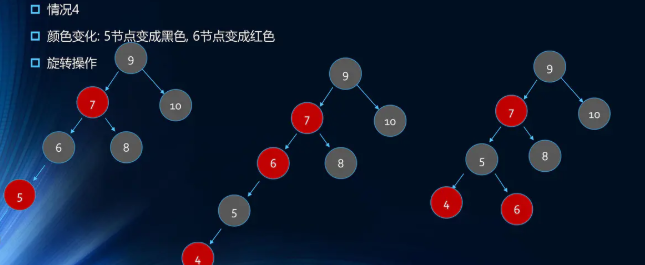
- 插入4
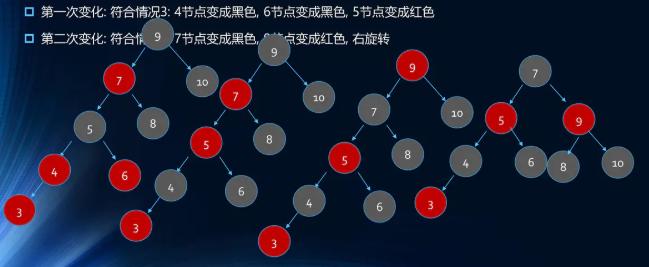
- 插入3
- 插入2
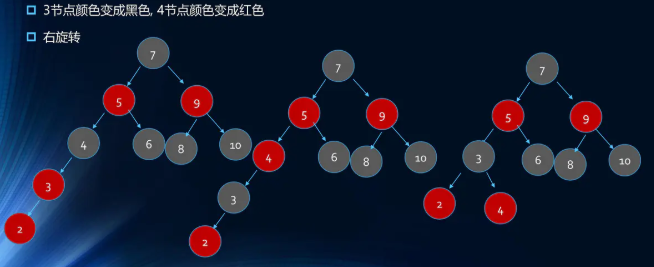
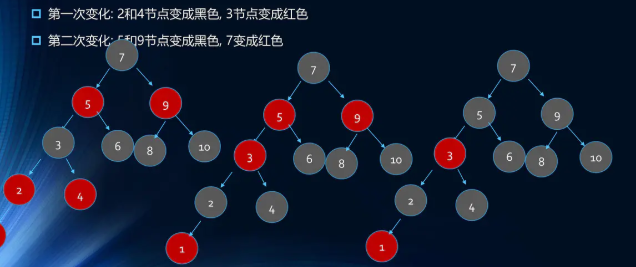
- 插入1
转自coderwhy:https://www.jianshu.com/p/00aae4f4d672

1
1
1
1
1
1
1
1
1
1